- Quiz will start as soon as you click the ‘Start Quiz‘ button below.
- Question will come one by one click on next for next question
- There are 30 questions in this quiz, you will get 30 Minutes to attempt.
- 2 Marks is determined for the correct answer for each question. There is no negative marking for incorrect answer.
- After the quiz is over, in order to know your rank in the Ranking List / Leader-board below, you should enter your name and email address, otherwise you will be deprived of it.
- After completing click on finish Quiz
- To see correct answers click on view Question
- जैसे ही आप नीचे दिए गए ‘स्टार्ट क्विज़’ बटन पर क्लिक करेंगे, क्विज़ शुरू हो जाएगा।
प्रश्न अगले प्रश्न के लिए अगले एक क्लिक पर आएगा
इस क्विज में 30 प्रश्न हैं, आपको प्रयास करने के लिए 30 मिनट मिलेंगे।
प्रत्येक प्रश्न के सही उत्तर के लिए 2 अंक निर्धारित किए गए हैं। गलत उत्तर के लिए कोई नकारात्मक अंकन नहीं है।
प्रश्नोत्तरी समाप्त होने के बाद, नीचे दी गई रैंकिंग सूची / लीडर-बोर्ड में अपनी रैंक जानने के लिए, आपको अपना नाम और ईमेल पता दर्ज करना चाहिए, अन्यथा आप इससे वंचित रह जाएंगे।
फिनिश क्विज़ पर क्लिक करने के बाद
सही उत्तर देखने के लिए प्रश्न पर क्लिक करें
Paper 2 CS Discrete Structures and Optimization Part 1
Quiz-summary
0 of 30 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
Information
Paper 1 Quiz helps u to Excel in NET JRF
Paper 1 All questions 2 Marks each
- Navdeep Kaur
- All the Best
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
0 of 30 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Categories
- Not categorized 0%
- CS 1 Discrete Structures and Optimization 0%
-
Average marks Improve next time All the Best
-
Nice Keep it up, Stay Blessed
-
Awesome Great Marks, Keep doing
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Answered
- Review
-
Question 1 of 30
1. Question
2 pointsCategory: CS 1 Discrete Structures and OptimizationIn Propositional Logic, given P and P → Q, we can infer __________
Correct
Modus ponens rule / Rule of detachment: According to Modus ponens rule given P and P → Q, we can infer Q
Incorrect
Modus ponens rule / Rule of detachment: According to Modus ponens rule given P and P → Q, we can infer Q
-
Question 2 of 30
2. Question
2 points“Consider the following logical inferences :
I1 : If it is Sunday then school will not open.
The school was open.
Inference : It was not Sunday.
I2 : If it is Sunday then school will not open.
It was not Sunday.
Inference : The school was open.
Which of the following is correct ? “Rules of Inteference!Correct
Rules of Inteference!
Incorrect
Rules of Inteference!
-
Question 3 of 30
3. Question
2 points“Let ν(x) mean x is a vegetarian, m(y) for y is meat, and e(x, y) for x eats y. Based on these, consider the following sentences :
I. ∀x ν(x ) ⇔ (∀y e(x, y) ⇒ ¬m(y))
II. ∀x ν(x ) ⇔ (¬(∃ym(y) ∧e(x, y)))
III. ∀x (∃y m(y) ∧e(x, y)) ⇔ ¬ν(x)
One can determine that “Correct
Rules of Inteference!
Incorrect
Rules of Inteference!
-
Question 4 of 30
4. Question
2 pointsConsider a source with symbols A, B, C, D with probability 1/2, 1/4, 1/8, 1/8 respectively. What is the average number of bits per symbol for the Huffman code generated from above information ?
Correct
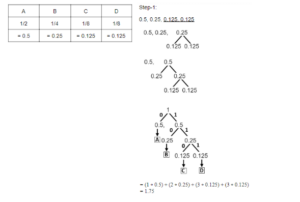
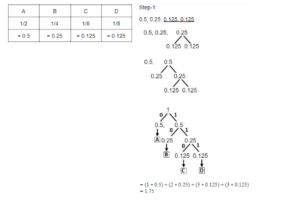Incorrect
-
Question 5 of 30
5. Question
2 points“The symmetric difference of two sets S1 and S2 is defined as
S1⊖S2 = {x|x ∈ S1 or x ∈ S2, but x is not in both S1 and S2}
The nor of two languages is defined as nor (L1, L2) = {w|w |∈L1 and w |∈ L1}.
Which of the following is correct?”
Correct
Incorrect
-
Question 6 of 30
6. Question
2 pointsThe first order logic (FOL) statement ((R ∨ Q) ∧ (P ∨ ¬Q)) is equivalent to which of the following ?
Correct
“Boolean simplification
((R ∨ Q) ∧ (P ∨ Q’))
(R∨Q)∧(P∨Q’)∧(R∨P)
(PR ∨ Q’R ∨ PQ) ∧ (R∨P)
PR ∨ RQ’ ∨ PQR ∨ PR ∨ PRQ’ ∨ PQ
(RQ’∨PQ’R)∨(PQR∨PQ)∨PR
RQ’ ∨ PQ ∨ PR
((R ∨ Q) ∧ (P ∨ Q’) ∧ (R ∨ P)) “Incorrect
“Boolean simplification
((R ∨ Q) ∧ (P ∨ Q’))
(R∨Q)∧(P∨Q’)∧(R∨P)
(PR ∨ Q’R ∨ PQ) ∧ (R∨P)
PR ∨ RQ’ ∨ PQR ∨ PR ∨ PRQ’ ∨ PQ
(RQ’∨PQ’R)∨(PQR∨PQ)∨PR
RQ’ ∨ PQ ∨ PR
((R ∨ Q) ∧ (P ∨ Q’) ∧ (R ∨ P)) “ -
Question 7 of 30
7. Question
2 pointsSuppose there are n stations in a slotted LAN. Each station attempts to transmit with a probability P in each time slot. The probability that only one station transmits in a given slot is _______.
Correct
This question can be solved by binomial distribution
Incorrect
This question can be solved by binomial distribution
-
Question 8 of 30
8. Question
2 points“Consider the following two well-formed formulas in propositional logic.
F1 : P ⇒ ¬ P
F2 : (P ⇒ ¬ P) ∨ (¬ P ⇒ P)
Which of the following statements is correct? “Correct
Incorrect
-
Question 9 of 30
9. Question
2 points“If X, then Y unless Z” is represented by which of the following formulae in propositional logic?
Correct
“””If X then Y unless Z”” ⇒ ¬Z → (X→Y)
⇒ Z ∨ ¬X ∨ Y
⇒ ¬X ∨ Z ∨ Y
Option B: (X ∧ ¬Z) → Y
= ¬(X ∧ ¬Z ) ∨ Y
= ¬X ∨ Z ∨ Y
Hence, option is correct. “Incorrect
“””If X then Y unless Z”” ⇒ ¬Z → (X→Y)
⇒ Z ∨ ¬X ∨ Y
⇒ ¬X ∨ Z ∨ Y
Option B: (X ∧ ¬Z) → Y
= ¬(X ∧ ¬Z ) ∨ Y
= ¬X ∨ Z ∨ Y
Hence, option is correct. “ -
Question 10 of 30
10. Question
2 pointsLet P, Q, R and S be Propositions. Assume that the equivalences P ⇔ (Q ∨ ¬ Q) and Q ⇔ R hold. Then the truth value of the formula (P ∧ Q) ⇒ ((P ∧ R) ∨ S) is always:
Correct
Incorrect
-
Question 11 of 30
11. Question
2 pointsThe logic of pumping lemma is an example of __________.
Correct
“→ A pumping lemma (or) pumping argument states that, for a particular language to be a member of a language class, any sufficiently long string in the language contains a section, or sections, that can be removed, or repeated any number of times, with the resulting string remaining in that language.
→ The proofs of these lemmas typically require counting arguments such as the pigeonhole principle.
→ Hence, the logic of pumping lemma is a good example of the pigeonhole principle. “Incorrect
“→ A pumping lemma (or) pumping argument states that, for a particular language to be a member of a language class, any sufficiently long string in the language contains a section, or sections, that can be removed, or repeated any number of times, with the resulting string remaining in that language.
→ The proofs of these lemmas typically require counting arguments such as the pigeonhole principle.
→ Hence, the logic of pumping lemma is a good example of the pigeonhole principle. “ -
Question 12 of 30
12. Question
2 pointsA WFF that is equivalent to the WFF x=>y is :
Correct
WFF means well formed formula. Just draw truth table and you will see option C is correct
Incorrect
WFF means well formed formula. Just draw truth table and you will see option C is correct
-
Question 13 of 30
13. Question
2 pointsThe number of edges in a complete graph with ‘n’ vertices is equal to :
Correct
Theorem : Complete graph is an undirected graph in which each vertex is connected to every vertex, other than itself. If there are ‘n’ vertices then total edges in a complete graph is n(n-1)/2.
Incorrect
Theorem : Complete graph is an undirected graph in which each vertex is connected to every vertex, other than itself. If there are ‘n’ vertices then total edges in a complete graph is n(n-1)/2.
-
Question 14 of 30
14. Question
2 pointsA box contains six red balls and four green balls. Four balls are selected at random from the box. What is the probability that two of the selected balls are red and two are green ?
Correct
Incorrect
-
Question 15 of 30
15. Question
2 pointsAn example of a tautology is :
Correct
Draw the truth table and C is the answer. Its a very simple question.
Incorrect
Draw the truth table and C is the answer. Its a very simple question.
-
Question 16 of 30
16. Question
2 pointsIn a set of 8 positive integers, there always exists a pair of numbers having the same remainder when divided by :
Correct
“Given data,
— Set of positive integers=8
— A pair of numbers having the same remainder when divided by=?
Step-1: This problem, we can use pigeonhole principle.
Pigeonhole Principle: If there are ‘X’ positive integers to be placed in ‘Y’ possible remainder where Y < X, then there is at least one possible remainder which receives more than one positive integer. Option-A: Total number of possible remainders, divided by 7 is 0,1,2,3,4,5,6. These numbers are less than 8 only. Option-B,C and D: Total number of possible remainders, divided by 11, 13, 15 is greater than 8 "Incorrect
“Given data,
— Set of positive integers=8
— A pair of numbers having the same remainder when divided by=?
Step-1: This problem, we can use pigeonhole principle.
Pigeonhole Principle: If there are ‘X’ positive integers to be placed in ‘Y’ possible remainder where Y < X, then there is at least one possible remainder which receives more than one positive integer. Option-A: Total number of possible remainders, divided by 7 is 0,1,2,3,4,5,6. These numbers are less than 8 only. Option-B,C and D: Total number of possible remainders, divided by 11, 13, 15 is greater than 8 " -
Question 17 of 30
17. Question
2 pointsThe set of positive integers under the operation of ordinary multiplication is :
Correct
The set of positive integers under the operation of ordinary multiplication is a monoid but not a group.
Incorrect
The set of positive integers under the operation of ordinary multiplication is a monoid but not a group.
-
Question 18 of 30
18. Question
2 pointsA relation R in {1, 2, 3, 4, 5, 6} is given by { (1, 2), (2, 3), (3, 4), (4, 4), (4, 5) }. This relation is :
Correct
“Reflexive: A relation R is said to be reflexive if for all elements of a set x belongs to R (x,x) exists. \n
Since in above question {(1,1), (2,2),(3,3),(4,4),(5,5),(6,6)} does not exist in given relation so it is not reflexive. \n
Symmetric: A relation R is symmetric if (x,y) belong to R then (y,x) must belong to R. Since in above question (1,2) exists but (2,1) does not exist in given relation so given relation is not symmetric. \n
Transitive: A relation is transitive if (x,y) belongs to R and (y,z) belongs to R then (x,z) must belongs to R. \n
In above question (1, 2), (2, 3) exist in given relation but (1,3) does not exist there so given relation is not transitive. \n
Hence correct option is option \n”Incorrect
“Reflexive: A relation R is said to be reflexive if for all elements of a set x belongs to R (x,x) exists. \n
Since in above question {(1,1), (2,2),(3,3),(4,4),(5,5),(6,6)} does not exist in given relation so it is not reflexive. \n
Symmetric: A relation R is symmetric if (x,y) belong to R then (y,x) must belong to R. Since in above question (1,2) exists but (2,1) does not exist in given relation so given relation is not symmetric. \n
Transitive: A relation is transitive if (x,y) belongs to R and (y,z) belongs to R then (x,z) must belongs to R. \n
In above question (1, 2), (2, 3) exist in given relation but (1,3) does not exist there so given relation is not transitive. \n
Hence correct option is option \n” -
Question 19 of 30
19. Question
2 pointsThe graph K3,4 has :
Correct
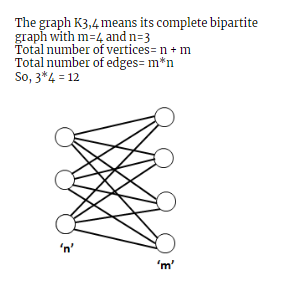Incorrect
-
Question 20 of 30
20. Question
2 pointsThe number of edges in a complete graph of n vertices is
Correct
Theorem : Complete graph is an undirected graph in which each vertex is connected to every vertex, other than itself. If there are ‘n’ vertices then total edges in a complete graph is n(n-1)/2.
Incorrect
Theorem : Complete graph is an undirected graph in which each vertex is connected to every vertex, other than itself. If there are ‘n’ vertices then total edges in a complete graph is n(n-1)/2.
-
Question 21 of 30
21. Question
2 pointsIf she is my friend and you are her friend, then we are friends. Given this, the friend relationship in this context is ____________. (i) commutative (ii) transitive (iii) implicative (iv) equivalence
Correct
“→ Initially calculate the possible cases of a relation i.e., R={(A,B), (C,B), (A,C)} \n
→ Now check whether the relation is transitive or commutative or etc.., \n
If a relation is commutative then if (A,B) present in the relation then (B,A) also need to exists. but in the relation (B,A) is not present. so given relation is not commutative. \n”Incorrect
“→ Initially calculate the possible cases of a relation i.e., R={(A,B), (C,B), (A,C)} \n
→ Now check whether the relation is transitive or commutative or etc.., \n
If a relation is commutative then if (A,B) present in the relation then (B,A) also need to exists. but in the relation (B,A) is not present. so given relation is not commutative. \n” -
Question 22 of 30
22. Question
2 points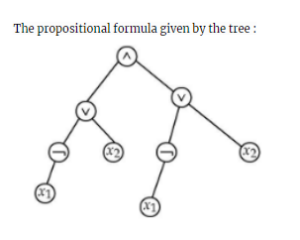
Correct
“By default we are using inorder traversal to evaluate it.
Inorder traversal starts from left,root and right.
Inorder traversal = (¬x1∨ x2) ∧ (¬x1∨ x2) “Incorrect
“By default we are using inorder traversal to evaluate it.
Inorder traversal starts from left,root and right.
Inorder traversal = (¬x1∨ x2) ∧ (¬x1∨ x2) “ -
Question 23 of 30
23. Question
2 points“Which two of the following are equivalent for an undirected graph G ?
(i) G is a tree
(ii) There is at least one path between any two distinct vertices of G
(iii) G contains no cycles and has (n-1) edges
(iv) G has n edges “Correct
“Option-i: FALSE because undirected graph will be cycle also.
Option-ii: TRUE because there is at least one path between any two distinct vertices of G. otherwise we are no calling as undirected graph.
Option-iii: TRUE. If G contains no cycles and has (n-1) edges.
Option-iv: FALSE “Incorrect
“Option-i: FALSE because undirected graph will be cycle also.
Option-ii: TRUE because there is at least one path between any two distinct vertices of G. otherwise we are no calling as undirected graph.
Option-iii: TRUE. If G contains no cycles and has (n-1) edges.
Option-iv: FALSE “ -
Question 24 of 30
24. Question
2 pointsThe complete graph with four vertices has k edges where k is :
Correct
“To find number of edges in complete graph using standard formula is n(n-1)/2. Here, n=4
= 4(4-3)/2
= (4*3)/2
= 12/2
= 6 “Incorrect
“To find number of edges in complete graph using standard formula is n(n-1)/2. Here, n=4
= 4(4-3)/2
= (4*3)/2
= 12/2
= 6 “ -
Question 25 of 30
25. Question
2 pointsIf x and y are independent Gaussian random variables with average value 0 and with same variance, their joint probability density function is given by :
Correct
“As they are independent, answer could be Option-A, though it need to be checked with zero average too.
Note: Original key given option-C is correct answer . NET 2009”Incorrect
“As they are independent, answer could be Option-A, though it need to be checked with zero average too.
Note: Original key given option-C is correct answer . NET 2009” -
Question 26 of 30
26. Question
2 points“S1 : I teach algorithms and maths.
S2 : My professor teaches maths, electronics and computer science.
S3 : I have a student of maths.
S4 : Algorithm is a part of computer science.
S5 : Maths students know computer science.
What would be the chromatic number of a graph, vertices of which are the actors/entities that are involved in the sentences S1 to S5 and edges-to represent the associations/relationships amongst the entities/actors as expressed in the sentences S1 to S5 above ?”Correct
Solve using graph theory
Incorrect
Solve using graph theory
-
Question 27 of 30
27. Question
2 points“x1 is a clone of x” means x1 is identical to x in terms of the physical attributes namely, height, weight and complexion. Given, height, weight and complexion only form a complete set of attributes for an entity, cloning is an equivalence relation. What is your impression about this statement ?
Correct
“The given statement says that the Relation R contains x and x1 which are identical. Which means (x,x1) are same as (x,x).
We know that “” a relation of (x,x) type is an equivalence as it satisfies Reflexive, symmetric, transitive.
The answer would be option A, it is equivalence. “Incorrect
“The given statement says that the Relation R contains x and x1 which are identical. Which means (x,x1) are same as (x,x).
We know that “” a relation of (x,x) type is an equivalence as it satisfies Reflexive, symmetric, transitive.
The answer would be option A, it is equivalence. “ -
Question 28 of 30
28. Question
2 pointsThe value of the following expression (13 / 4 * 3) % 5 + 1 is
Correct
“(13 / 4 * 3) % 5 + 1
Step-1: (13 / 4 * 3) % 5 + 1
Step-2: (3.25*3)%5+1
Step-3: 9.75%5+1
Step-4: 4.75+1
Step-5: 5.75
Note: ( ) having highest precedence then *,/ and % have same precedence order. “Incorrect
“(13 / 4 * 3) % 5 + 1
Step-1: (13 / 4 * 3) % 5 + 1
Step-2: (3.25*3)%5+1
Step-3: 9.75%5+1
Step-4: 4.75+1
Step-5: 5.75
Note: ( ) having highest precedence then *,/ and % have same precedence order. “ -
Question 29 of 30
29. Question
2 pointsThe minimum number of edges in a connected graph with ‘n’ vertices is equal to
Correct
For connected graph : Maximum is n(n-1)/2 and minimum is n – 1
Incorrect
For connected graph : Maximum is n(n-1)/2 and minimum is n – 1
-
Question 30 of 30
30. Question
2 pointsA partially ordered set is said to be a lattice if every two elements in the set have
Correct
“A partially ordered set is said to be a lattice if every two elements in the set have
1. Unique least upper bound
2. Unique greatest lower bound “Incorrect
“A partially ordered set is said to be a lattice if every two elements in the set have
1. Unique least upper bound
2. Unique greatest lower bound “
- Next Quiz on Paper 1 Daily at navclasses.in 12 PM
- Commerce Paper 2 Sunday at navclasses.in
- Computer Science Paper 2 Sunday at navclasses.in
- Economics Paper 2 Sunday at navclasses.in
- Education Paper 2 Sunday at navclasses.in
Study Paper 1 Topics for Free Click Here
eBook Combo Computer Science and Applications Complete Guide + Question Bank
Get subscription for Complete Preparation NTA NET JRF: https://unacademy.com/subscribe/TEWDQ
use my referral code for 10% additional discount: NAVCLASSES
Search Navdeep Kaur and start watching ongoing courses
Leaderboard: Paper 2 CS Discrete Structures and Optimization Part 1
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
One Response
Levitra Acheter [url=https://cheapcialisir.com/#]Cialis[/url] Xenical Fat Blocker Cialis Amoxicillin Elixir